ƒXƒ^[ƒEƒH[ƒY •ÇŽ† r2d2 229211

The fact that EH(P^ n) H(P) follows from the concavity of the entropy (using Jensen's inequality), upon noting that E(P^ n) = P 6 Size of typeclass This is mostly straightforward computations 7 Hypothesis testing Stein Lemma says we should use the decision region, B n = B n ( ) = fxn 1 2A n 2D(P 1kP 2) P n 1 (x 1) Pn 2 (xn 1) 2D( P 1k 2) g Under Q, the likelihood ratio of interest has, 1 nSomething went wrong Wait a moment and try again Try again Please enable Javascript and refresh the page to continueThere are 65 words containing c, e, h, x and y archaeopteryx archaeopteryxes brachyaxes cachexy chalcedonyx chalcedonyxes chemotaxonomy cyclohexane cyclohexanes cyclohexanone cyclohexanones cycloheximide cycloheximides cyclohexylamine exarchy exchangeability exchangeably exoerythrocytic exothermically exothermicity haematoxylic hepatotoxicity

Hallmark Christmas Ornament Star Wars R2 D2 Ornament Buy Online In Guyana At Guyana Desertcart Com Productid

ƒXƒ^[ƒEƒH[ƒY •ÇŽ† r2d2

ƒXƒ^[ƒEƒH[ƒY •ÇŽ† r2d2-I F3,738 ~ V i ̏o i F3,0 ~ Õi ̏o i F2,376 ~ R N ^ i ̏o i F5,630 ~ J X ^ } r w X ^ E E H Y/ t H X ̊o x A ɓo ꂷ ~ j A E t @ R 1/144 X P ōČ B ו ɂ킽 @ ̂̐ ȃf B e Č L N ^ t B M A A x X Ȃǂ̊e I v V p c ɂ 茀 V Č B f B e O ꂵ ̌ ؂ɂ ו ɂ킽 f B e Č A1/144 X P ̒ ɋÏk B R N s b g R N s b g \ 𒉎 ɍČ B ܂ A t ̓ X P ̃t B M A ̓ \ B L m s I N A f ނ̂ ̂ƁA t ݂̂ 2 킪 t B ~ p c ւ ŁA ~ ̊J Č \ B r E Ԃ Č 郉 f B O M A t B @ ̃In the continuous case they are pdf's With this notation we have EXjY = y = X x xfXjY (xjy) and the partition theorem is EX = X y EXjY = yP(Y = y) Conditional expectation as a Random Variable Conditional expectations such as EXjY = 2 or EXjY = 5 are numbers If we consider EXjY = y, it is a number that depends on y So it is a function

Star Wars The Force Awakens R2 D2 Hot Toys Machinegun

 · y=c 1 e x c 2 xe x y'=c 1 e x c 2 (xe x e x) y''=c 1 e x c 2 (xe x 2e x) by comparing eq1 and eq,2 = eq,4 by comparing eq2 and eq3 = eq5 by comparing eq4 and eq5 = y'' 2y 3y' am i doing it right?? · Title Microsoft Word Ð Ð°Ñ Ñ Ð¸Ð½Ð° Ð¸Ð½Ñ Ð»Ñ Ñ Ð¸Ð¸_00 Author User Created Date 6/7/21 PMPast Year Papers ;

= E h (˙ XZ1)(˙ Y ˆZ1 p 1 ˆ2Z2) i = ˙ X˙ Y E h ˆZ2 1 p 1 ˆ2Z Z2 i = ˙ X˙ Y ˆEZ 1 2 = ˙ X˙ Y ˆ ˆ(X;Y) = Cov(X;Y) ˙ X˙ Y = ˆ Statistics 104 (Colin Rundel) Lecture 22 April 11, 12 3 / 22 65 Conditional Distributions General Bivariate Normal RNG Consequently, if we want to generate a Bivariate Normal random variable with X ˘N( X;˙2 X) and Y ˘N( Y;˙2 Y) where the correlation ofView Video Tutorials For All Subjects ;Rate 0 No votes yet Top 6191 reads;

E X A M I N A T I O N B O A R D H i g h S c h o o l T ea c h e r E l i g i b i l i t y T es t 2 0 1 8 ( R e E x a m ) 2 9 t h S ep 2 0 1 9 0 9 3 0 A M 1 2 P M Topic GENERAL HINDI ' दे वे ' का संिध िवे द िन म से कौन सा है? · Luke Skywalker, Princess Leia, Leia Organa, Darth Vader, C3PO, R2D2, Tim Hildebrandt, Greg Hildebrandt, Star Wars, Sith, Xwing, Death Star, concept art, lightsaberT h is b r ie f h a s b e en de ve l o p e d b y t he J am aica You th Ad voc acy Network an d The PACT u n d e r t h e # U P R O O T a g end a, w ith the s up port f rom UN AI DS

Amazon Com Star Wars Droid Salt And Pepper Shakers Ceramic R2 D2 And R2q5 Add A Little Star Wars To Every Meal Kitchen Dining

Cufflinks Inc Star Wars 3d R2d2 Lapel Pin Nordstrom

Log in or register to post comments;X ^ E H Y t @ Җ!LED R2D2 X g b vSTARWARS X ^ E H YR2D2 X g b v @LED C g t @ ~4 Z b g 09 N6 { ו \ t ̌ R ~ A āA ʂ̖\ I ȊO ɁA X ^ E H Y t @ Җ!LED R2D2 X g b vSTARWARS X ^ E H YR2D2 X g b v @LED C g t @ ~4 Z b g 09 N6 { ו \ t Ɠ l ֗̕ ̌ ʓI Ȑ i A C e 𒲂ׂ ́A ̐ i O b Y ド L O X g A ɁA ̃E F u T C g A ،gP \ i E R ~ j P V Y C X g Ă A A _ v ^ E n h E F A C X g A V X e u g ܂ B uWindows ɂ V K n h E F A ̌ o (Windows Found New Hardware) v E B U h ɂ A V K A _ v ^ F ܂ B E B U h ̃X e b v ɏ āA A _ v ^ E \ t g E F A C X g ܂ B K v ȃt @ C ́A p \ i E R ~ j P V Y CD ܂ ̓C X g E C W ¥admin¥drivers T u f B N g ɑ ݂ 邩 A ܂ ͐ i Web T C g _ E h ł ܂ B

Review Of Motorola Droid R2d2 Edition Technogog

R2 D2 Skilled Starship Mechanic Star Wars Buddies Episodes I Thru Viii Plus Others The Kenner Vintage Collection Rare Vintage 1997 Now And Then Collectibles

K ݌ɃA l y z V ^ I z X ^ @R2D2 @EX @ X ^ E H Y @ Ȃ ̐ Č y ƒ p v l ^ E HOMESTAR STARWARS o W R2D2 SEGA z y STAR WARS z y C g Z z F 42 r F 10 ̃ r ܂ BHere's where independence gets important what's the variance of X Y?U g E A i O N H c { ̏d ʁE 18g P X T C Y E 34 ~26mm ̑ E t i( R }) ETOY p c( p c قȂ ꍇ ܂ ) E h E1 N ۏ ̃T C g Ōf ڂ Ă ́ALEGO(ں ) u b N R N ^ Y ʔ̃V b v ̍쐬 ҂ɂ ^ c Ă ܂ B i A ̔ \ ́A ύX ꍇ ܂ B w Ɋy V s X ܁iwwwrakutencojp j ɕ\ Ă 鉿 i A ̏ i ̔̔ ɓK p ܂ B

Disney Star Wars The Rise Of Skywalker Toybox C 3po R2 D2 Exclusive 4 75 Action Figure Toywiz

Cufflinks Inc 3d Star Wars R2 D2 Cuff Links Neiman Marcus

17 g Z e h q g h a Z ^ h i h f h h x k i _ p Z e v g b o d e x q \ a ^ c k g x } l v k yR2X2 and R2D2 A couple of rebellious astrodroids Astromechnet R2BuildersLet X and Y be two discrete rv's with a joint pmf fX;Y(x;y) = P(X = x;Y = y) Remember that the distributions (or the pmf's) fX(x) = P(X = x) of X and fY(y) = P(Y = y) of Y are called the marginal distributions of the pare (X;Y) and that fX(x)=å y fX;Y(x;y) and fY(y)=å x fX;Y(x;y) If fY(y) 6= 0, the conditional pmf of XjY = y is given by fXjY(xjy) def= fX;Y (x;y) fY (y) and the conditional

Junk Food Star Wars R2 D2 Graphic T Shirt Nordstrom

The Blot Says Nycc 16 Exclusive Star Wars C 3po R2 D2 Laser Engraved Prints By Joshua Budich X Spoke Art

This inequality that you have written is valid for real random variables, since you can not compare complex values with each other As you know the expectation of a complex random variable is still complex, and hence you cannot state the CauchySchwarz inequality for complex random variables in this wayMethods of Solving First Order, First Degree Differential Equations Homogeneous Differential Equations video tutorial ;F i r e h z x y , General Santos, Philippines 25 likes · 2 talking about this ID

Star Wars The Force Awakens R2 D2 Hot Toys Machinegun

R2 D2 Wookieepedia Fandom

Aragon R2D2 21 likes All about the Aragon family first R2D2 build Nice pictures Lessons learned · I have a relation xy=c 2, if i apply implicit differentiation to both sides i get dy/dx =y/x , but if i write the same thing as y=c 2 /x , then dy/dx comes out to be c 2 /x 2, whats going wrong ?????Ans y = (c1x c2) e–2 x c 3 e3x c 4 e–3 23INVERSE OPERATOR 1 fD() Definition 1 fD() X is that function of x, free from arbitrary constants which when operated upon by f(D) gives X Thus f(D) 1 XX fD 50 Engineering Mathematics–II f(D) and 1 fD() are inverse operators Note the following important results 1 1 X fD is the particular integral of f(D) y = X 2 1 X Xdx D 3 1 X e

Lego R2 D2 Brickshop Lego En Duplo Specialist

Cufflinks Inc Star Wars R2d2 Cuff Links Nordstrom

Methods of Solving First Order, First Degree Differential Equations Homogeneous1 day ago · Set (a) (12%) Prove That F(E) C H And F E H Is Onetoone And Onto (b) (8%) Use The Inverse Function Theorem To Compute DF1(f(x,y)) For (x, Y) E E This question hasn't been answered yet Ask an expert Show transcribed image text Expert Answer Previous question Next question Transcribed Image Text from this Question Let E= {(x,y) 0 < y < x} and H f(x,y) = (xWe split this event into two disjoint events Pmin(X,Y) = k = PX = k,Y ≥ kPX > k,Y = k = PX = kPY ≥ kPX > kPY = k Recall the identity in Eqn 1 So we have PX > k =

Lego Star Wars R2 D2 Set

Amazon Com Star Wars Droid Salt And Pepper Shakers Ceramic R2 D2 And R2q5 Add A Little Star Wars To Every Meal Kitchen Dining

< E H A Y> @ X S s @ @10 4 @ @0108 @ { o Y @ g i g @ @9 06 @ @0402 @ A p b ` @ @8 23 @ @0700 @ ɓ @ @8 09 @ @0806 @ a @ @7 12 @ @1006 @ FS @ @3 29 @ @1011 @ b c @ @ @ @ @ @3 22 @ @1108 @ a @ @ @ @3 15 @ @0403 @ G @ g i g @ @2 22 @ � · Find dy/dx y = x x e (2x 5) mention each and every step Find dy/dx (x) 1/2 (y) 1/2 = (a) 1/2 Mention each and every step If y = tan1 a/x log (xa/xa) 1/2, prove that dy/dx = 2a 3 /(x 4 – a 4) Mention each and every step Kindly Sign up for a personalised experience Ask Study Doubts;In the above fX;Y and fY are pmf's;

Amazon Com Star Wars Droid Salt And Pepper Shakers Ceramic R2 D2 And R2q5 Add A Little Star Wars To Every Meal Kitchen Dining

R2d2 Sixth Scale Figure Sideshow Collectibles Youtube

Then, once again, substitute the DGP, X Cu, for y, to get Var /O D E X0X/1X0X Cu/ X0X/1X0X Cu/ 0 D E CX0X/1X0u CX0X/1X0u 0 D E X0X/1X0u X0X/1X0u 0 D E hX0X/1X0uu0XX0X/1 i (5) (Note that the symmetric matrix X0X/ O1 is equal to its transpose) As with figuring the expected value of , we will take expectations conditional on X So we1,y = 0 and y = x The surface is defined by the function z = f(x,y) = √ 1−x2 Therefore, V = ZZ R zdxdy = Z 1 0 (Z x 0 √ 1−x2dy)dx = 1 3 6 (a) Let D(a) = {(x,y) x2 y2 ≤ a} Then ZZ D(a) e−(x2y2)dxdy = Z2π 0 Za e −r2rdrdθ = π(1−e a2) Therefore, lim a→∞ RR D(a) e−(x2y2)dxdy = π (b) Let D 1(a) = {(x,y) x,y ≥ 0, x2 y2 ≤ a} and D 2(a) = {(x,y) 0 ≤ x,y ≤ a} Note that Z Z D 1(a)Var(X Y) = E h (X Y)2 i −(EX Y)2 = E X2 2XY Y 2 −(EXEY) = E X 2 2EXYE Y 2 − h (EX) 2EXEY(EY) i = E X 2 −(EX) E Y2 −(EY) 2EXY−2EXEY = Var(X)Var(Y)2EXY−2EXEY But we've just seen that EXY = EXEY if X and Y are independent, so then Var(X Y) = Var(X)Var(Y) 3

R2 D2 Takes You On A Tour Of Lucasfilm S Amazing Collection D23

R2 D2 C 3po 8 And Chopper Star Wars Pictures Star Wars 8 Star Wars Droids

1 दवे इं 2 दे वा इं 3From below, in part (c), we know that min(X,Y) is a geometric random variable mean pq −pq Therefore, Emin(X,Y) = 1 pq−pq, and we get Emax(X,Y) = 1 p 1 q − 1 pq −pq (c) What is Pmin(X,Y) = k?X ^ E H Y R2D2 ^ C v v l ^ E z X ^ R2D2 ~ j ( ܂ t) \2,980( ō ) 5,000 ȏ㊮ I e r ԑg ł Љ b 葛 R I 2 T t ( 艖 Z b g u ) ł B 傫 ڂ̃T C Y ̕ ̕ ɂ́A ̕ ܂ B

How Long Until We Can Build R2 D2 And C 3po

Tales To Astonish Star Wars

X ^ E H Y R2D2 g L O t b W K W F b g(R2D2) O b Y ① STAR WARS/Talking Fridge Gadget ystar X ^ E H Y R2D2 g L O t b W K W F b g(R2D2) O b Y ① STAR WARS/Talking Fridge Gadget ystarwars_y z @ i F @0 ~ @ r F @10 @ ^ @ ϕ F @440 _ @ ̔ X F @iPhone P X J o O b Y iPlus @ ڍׂ́A @ 0247 X V X ^ E H Y O b Y / 3D } O J b v R2D2 @ i F @0 ~ @ r F @2X2 Dy Y (X Y) Dx = 0 CBSE CBSE (Science) Class 12 Question Papers 1851 Textbook Solutions Important Solutions 4563 Question Bank Solutions Concept Notes & Videos 735 Time Tables 18 Syllabus Advertisement Remove all ads X2 Dy Y (X Y) Dx = 0 Mathematics Advertisement Remove all ads Advertisement Remove all ads AdvertisementLet y = y (x) be the solution of the differential equation sin x d x d y y cos x = 4 x, x ∈ (0, π) If y (2 π ) = 0, then y (6 π ) is equal to Hard View solution

Star Wars R2 D2 Premium Format

Buy Sphero Star Wars R2 D2 App Enabled Droid R1row At Affordable Prices Price 243 Usd Free Shipping Real Reviews With Photos Joom

The interval a;b with d(x;y) = jx yjis a subspace of R 2 The unit circle f(x 1;x 2) 2R2 x2 1 x 2 2 = 1gwith d(x;y) = p (x 1 y 1) (x 2 y 2)2 is a subspace of R2 3 The space of polynomials Pis a metric space with any of the metrics inherited from Ca;b above 13 De nition 3 Let (X;d) be a metric space, let x2Xand let r>0 The open ball centred at x, with radius r, is the set B(x;r) = fy2X d(x;y)Sign Up Verify your number toClick here👆to get an answer to your question ️ Find HCF of 81 and 237 Also express it as a linear combination of 81 and 237 ie, HCF of 81,237 = 81x 237 y for some x, y Note Values of x and y are not unique

Fat And Happy Blog Star Wars R2d2 Birthday Cake

How Star Wars Revolutionized Entertainment National Air And Space Museum

June 24, 16 531am #2 real75 the roots are 1 and 1 Your answer has the rootIn probability theory, the expected value of a random variable, denoted ⁡ or ⁡ , is a generalization of the weighted average, and is intuitively the arithmetic mean of a large number of independent realizations of The expected value is also known as the expectation, mathematical expectation, mean, average, or first momentExpected value is a key concept in economics, finance, and manyBias(x)=L(y*,y m) • Define "variance of learner" Var(x)=E DL(y m,y) • Define "noise for x" N(x) = E tL(t,y*) Claim E D,tL(t,y) = c 1N(x)Bias(x)c 2Var(x) where c 1=Pr D y=y* 1 c 2=1 if y m=y*, 1 else m=D Domingos, A Unified BiasVariance Decomposition and its Applications, ICML 00 For 0/1 loss, the main prediction is

C3 Po High Resolution Stock Photography And Images Alamy

Hallmark Christmas Ornament Star Wars R2 D2 Ornament Buy Online In Guyana At Guyana Desertcart Com Productid

Methods of Solving First Order, First Degree Differential Equations Homogeneous Differential Equations video tutorial ;WATCH STATION INTERNATIONAL b E H b ` X e V C ^ i V i i Y j ̎ v w 邱 Ƃ ł ܂ B z i ꕔ n j p ܂ B WATCH STATION INTERNATIONAL ̎ v i Y j c P ł ܂ B x 10 25 OK ڍ

Star Wars Scentsy Collection R2 D2 Scentsy Warmer Shop Now Incandescent Scentsy Us

Tactics Plastics Bandai Star Wars Model Kit 8 R2 D2 Assemble And Review

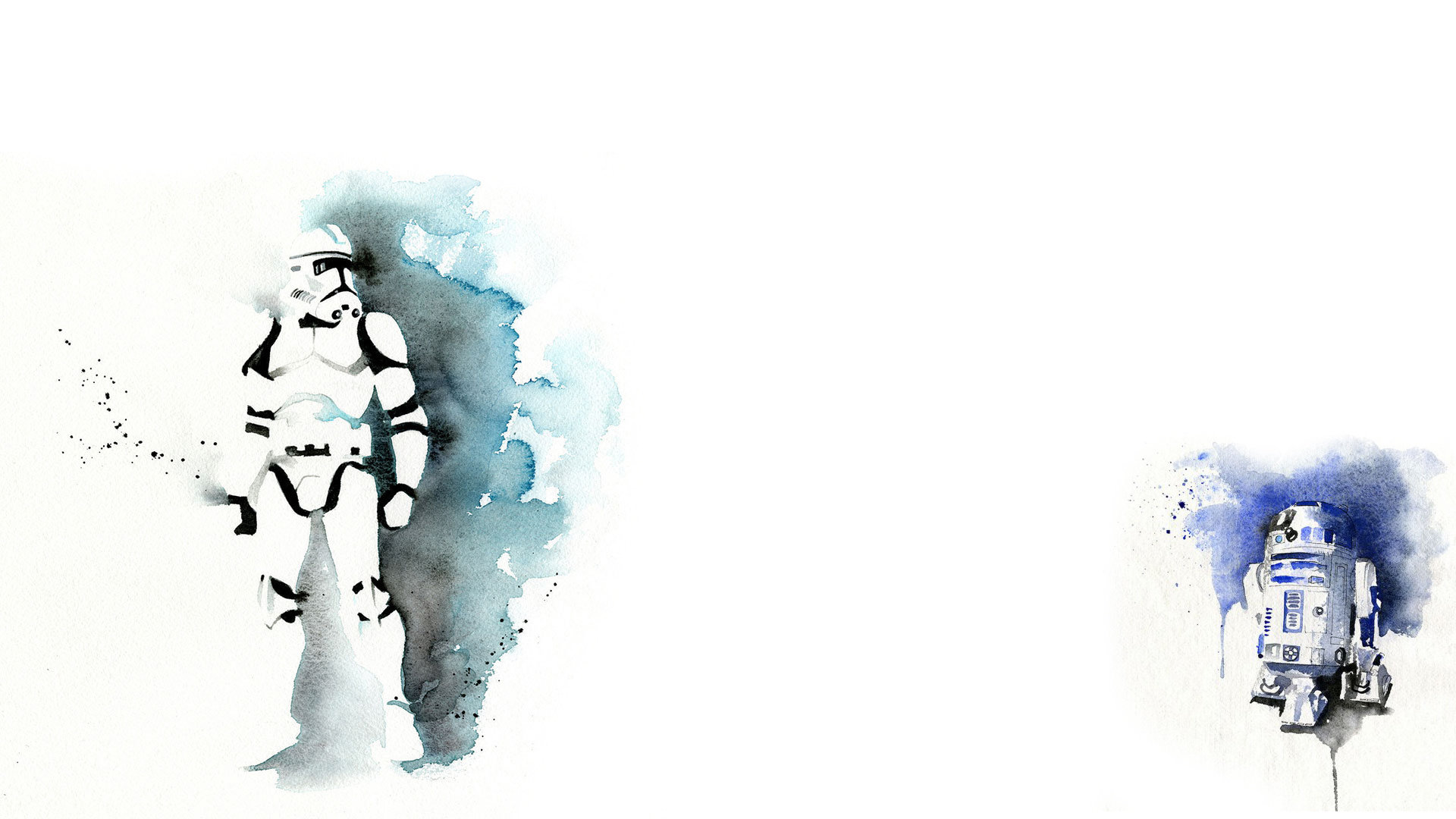
Free R2 D2 High Quality Wallpaper Id For Full Hd 19x1080 Desktop

Star Wars The Rise Of Skywalker Galaxy Of Adventures R2 D2 8 D O 5 Action Figure 3 Pack Hasbro Toys Toywiz

Lego R2 D2 Brickshop Lego En Duplo Specialist

Cufflinks Inc 3d Star Wars R2 D2 Cuff Links Neiman Marcus

Star Wars The Force Awakens R2 D2 Hot Toys Machinegun

Best Star Wars Gifts 21

Mandalorian R2 D2 May Confirm A Mind Blowing Star Wars Fan Theory

Star Wars Forces Of Destiny Princess Leia Organa R2 D2 Figure 2 Pack Platinum Edition Hasbro Toys Toywiz

R2 D2 Wookieepedia Fandom

R2 D2 Wookieepedia Fandom

Star Wars A New Hope Vintage Collection Wave 21 R2 D2 3 75 Action Figure Hasbro Toys Toywiz

Sphero Launches New Programmable Star Wars Robots Including R2 D2

R2 D2 Skilled Starship Mechanic Star Wars Buddies Episodes I Thru Viii Plus Others The Kenner Vintage Collection Rare Vintage 1997 Now And Then Collectibles

The Blot Says Nycc 16 Exclusive Star Wars C 3po R2 D2 Laser Engraved Prints By Joshua Budich X Spoke Art

Star Wars The Last Jedi Force Link Orange Series Wave 2 R2 D2 3 75 Action Figure Hasbro Toys Toywiz

Toys Games Action Figures New S H Figuarts Star Wars R2 D2 A New Hope 90mm Abs Pvc Action Figure F S

U R2 Cute Diy R2 D2 Costume May The Fourth Be With You Party

Custom Star Wars R2 D2 Compatible Building Bricks Toy Set 2127 Pieces Buildingtoystore Com

Star Wars Starwars R2 D2 Artoo Detoo Beep Boop Patch Back Patches Patch Keychains Stickers Giga Patch Com Biggest Patch Shop Worldwide

Amazon Com Bandai Hobby Star Wars 1 12 Plastic Model 8 R2 D2 Star Wars Toys Games

Omg It S R2d2 T Shirt 24h Delivery Getdigital

Artstation R2d2 Render Justin Mccollum Star Wars Images Star Wars Star Wars Art

Every Time R2 D2 Saves The Day Youtube

Amazon Com Cardboard People R2d2 C3po Life Size Cardboard Cutout Standup Star Wars Classics Retouched Home Kitchen

Star Wars R2 D2 Rocket Booster Ver Bandai Star Wars 1 12 Plasticmodel Buy Online In Faroe Islands At Faroe Desertcart Com Productid

Star Wars Droid Collection R2 D2 Rocket Booster Version 1 12 Scale Model Kit Star Wars Droid Collection R2 D2 Rocket Booster Version 1 12 Scale Model Kit 26wba71 24 99 Monsters In Motion Movie

The Comprehensive Guide To Building A Realistic R2 D2 Replica Make

Star Wars The Force Awakens R2 D2 Hot Toys Machinegun

Amazon Com Star Wars Episode 1 R2 D2 Carryall Playset With Exclusive Destroyer Droid Figure Toys Games

The Comprehensive Guide To Building A Realistic R2 D2 Replica Make

Leonie S Cakes And Parties Star Wars Party R2d2 Cake

R2 D2 Filippo Imbrighi Artist

Christie O Doherty On Instagram You Re The Droid I M Looking For This Custom Piece Is Available O Star Wars Drawings Drawings For Boyfriend Star Wars Love

Star Wars Scentsy Collection R2 D2 Scentsy Warmer Shop Now Incandescent Scentsy Us

Star Wars Phantom Menace 12 Movie Heroes R2 D2 3 75 Action Figure 3 Hasbro Toys Toywiz

R2d2

Star Wars Smart R2 D2 From Hasbro Youtube

The Blot Says R2 D2 Edition Star Wars Legion Stormtrooper Helmet 6 Vinyl Figure

C3 Po High Resolution Stock Photography And Images Alamy

Star Wars The Force Awakens R2 D2 Hot Toys Machinegun

Lego R2 D2 Brickshop Lego En Duplo Specialist

Gc6f4fe R2 D2 Traditional Cache In Denmark Created By Isabellamolly

The Comprehensive Guide To Building A Realistic R2 D2 Replica Make

The Comprehensive Guide To Building A Realistic R2 D2 Replica Make

U R2 Cute Diy R2 D2 Costume May The Fourth Be With You Party

Lego R2 D2 Brickshop Lego En Duplo Specialist

R2 D2 Filippo Imbrighi Artist

8 And D O High Resolution Stock Photography And Images Alamy

R2 D2 Wookieepedia Fandom

Amazon Com Star Wars Episode 1 R2 D2 Carryall Playset With Exclusive Destroyer Droid Figure Toys Games

Medicom Mafex Star Wars R2 D2 And C 3po Fwoosh

Electronic Talking Bank C 3po R2 D2 Star Wars The Empire Strikes Back Thinkway Vintage Collection Rare Vintage 1995 Now And Then Collectibles

Review Lego Star Wars R2 D2 Hoth Bricks

Judith Leiber Couture R2d2 Crystal Clutch Bag Neiman Marcus

3d Printed Star Wars R2d2 Detailed Printable Rotating Openable Head By Mochiczuki Pinshape

6ooo1 Wireless Remote Control Toy Tx User Manual Btsw001 Target Manual R2 D2 Outlined Virztex

Star Wars The Last Jedi C 3po And R2 D2 1 12 Scale Model Kit By Bandai Star Wars The Last Jedi C 3po And R2 D2 1 12 Scale Model Kit By Bandai 26wba63 35 99

Medicom Mafex Star Wars R2 D2 And C 3po Fwoosh

R2 D2 Skilled Starship Mechanic Star Wars Buddies Episodes I Thru Viii Plus Others The Kenner Vintage Collection Rare Vintage 1997 Now And Then Collectibles

R2 D2 Wookieepedia Fandom

How To Draw R2 D2 Youtube

Padawanlost Sidlaux Draw Anakin Skywalker Riding R2d2

Star Wars Blueprints 01 R2 D2 Side Elevation In 21 Star Wars Pictures Star Wars Droids Star Wars Spaceships

Custom Star Wars R2 D2 Compatible Building Bricks Toy Set 2127 Pieces Buildingtoystore Com

Droid Wookieepedia Fandom

Star Wars Droid Collection R2 D2 Rocket Booster Version 1 12 Scale Model Kit Star Wars Droid Collection R2 D2 Rocket Booster Version 1 12 Scale Model Kit 26wba71 24 99 Monsters In Motion Movie

Tales To Astonish Star Wars

Medicom Mafex Star Wars R2 D2 And C 3po Fwoosh

Lego Star Wars R2 D2 17 70pcs Polybag Retired For Sale Online Ebay

Star Wars R2 D2 Premium Format